MLF Lecture 4 Feasibility of Learning

Posted on Edited on Disqus:

機器學習基石(Machine Learning Foundations)笔记第三弹: 有限假说集合下 Machine Learning Possibility 的证明

Hoeffding's inequality（霍夫丁不等式）

N：样本容量υ：样本概率μ：总体概率

in big sample (N latge), v is probably close to \(\mu \color{coral}{\text{ (within }\epsilon)}\)

单一 Hypothesis 检验

  • Ein(h)：已知数据中 h 的错误率 \(\rightarrow \frac1N \sum_{n=1}^N[[h(x_n) \neq y_n]]\)
  • Eout：未知数据中 h 的错误率 \(\rightarrow \mathop\epsilon\limits_{x \sim p}[[h(x) \neq f(x)]]\)

由 Hoeffding's inequality 可以得，对单一的 hypothesis h，有

\[\begin{aligned} \mathbb{P}[\mid E_{in}(h) - E_{out}(h)\mid > \epsilon] \leq 2 exp(-2\epsilon^2N) \end{aligned}\]
  • 当 N 足够大时，有 Ein(h) ≈ Eout(h)
  • 所以可以通过 Ein(h) 推测 Eout(h) 从而可以通过 h(x)与已有数据 \(y_n\) 的吻合程度验证 how good it is

有限数量 Hypothesis 检验

  1. BAD Data:

    \(E_{in}(h)\) 和 \(E_{out}(h)\) 在该组数据上相差很大

    \[\begin{aligned} &\text{BAD data for many h} \\\ &\Longleftrightarrow \color{coral}{\text{no 'freedom of choice'}} \text{ by } \mathcal A \\\ &\Longleftrightarrow \color{coral}{\text{there exists some h such that } E_{out}(h) \text{ and } E_{in}(h) \text{ far away}} \end{aligned}\]

    ftrightarrow \end{aligned}

    BAD Data 令 A（Algorithm）不能自由地选择，即数据不够理想，A 不能完全根据已有数据检验 h 的好坏

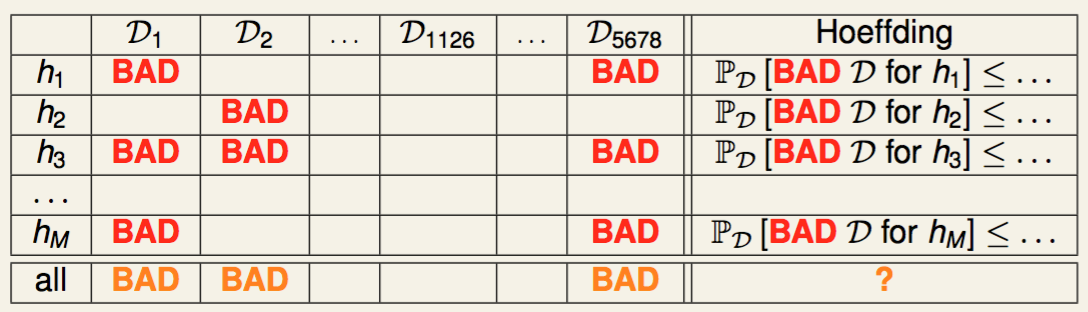
    对 M 个 Hypothesis \(\{h_1,h_2\dots,h_M\}\),如果存在任何一个 h 为 BAD，则该 Data 为 BAD

  2. BAD Data 出现概率上界

    \[\begin{aligned} \color{green}{\text{Bound of BAD Data}} \\\ \end{aligned}\]

    \end{aligned}

    \[\begin{aligned} &\mathbb P_D [ \color{coral}{\text{BAD }} D] \\\ = & \mathbb P_D [ \color{red}{\text{BAD }} D \text{ for } h_1 \textbf{ or } \mathbb P_D [ \color{red}{\text{BAD }} D \text{ for } h_2 \textbf{ or } \dots \mathbb P_D [ \color{red}{\text{BAD }} D \text{ for } h_M ] \\\ \leq & \mathbb P_D [ \color{red}{\text{BAD }} D \text{ for } h_1] + \mathbb P_D [ \color{red}{\text{BAD }} D \text{ for } h_2] + \dots + \mathbb P_D [ \color{red}{\text{BAD }} D \text{ for } h_M ] \text{(union bound)}\\\ \leq & 2exp(-2\epsilon^2N) + 2exp(-2\epsilon^2N) + \dots + 2exp(-2\epsilon^2N) \\\ = & 2 \color{coral}{M} exp(-2\epsilon^2N) \end{aligned}\]

    P_D [ D h_2] + + P_D [ D h_M ] \
    & 2exp(-2^2N) + 2exp(-2^2N) + + 2exp(-2^2N) \
    = & 2 exp(-2^2N) \end{aligned}

    • finite-bin version of Hoeffding, valid for all \(\color{coral}{M}\), N and \(\epsilon\)
    • does not depend on (therefore no need to know) any \(E_{out}(h_m)\)
    • ' \(E_{in}(g)=E_{out}(g)\) ' is \(\color{red}{PAC}\) (Probably approximately correct), regardless of \(\mathcal A\)
    • 'most reasonable' \(\mathcal A\) (like PLA/pocket): pick the \(h_m\) with \(\color{coral}{E_{in}(h_m)}\) as g

    因此，通过假设我们的所有数据（已知的和未知的）符合某一个分布，那么在有限 Hypothesis 的条件下，Machine Learning 被证明是可能的

    Statistical Learning Flow