红黑树实现（一）

Posted on Edited on Disqus:

Algorithms 4th RedBlackBST.java

红黑树介绍及其实现：概念，变换，插入结点实现

介绍

红黑树是一种通过将结点间链接分为红和黑两类，来实现与 「2-3 树」、「2-3-4 树」 等平衡树一一对应操作的平衡二叉树。查找、插入、删除复杂度均为 \(~lgN\) 。

本文中的红黑树实现基于 「2-3 树」，采取左倾的方式实现，链接的红黑属性记录于结点中，结点的颜色代表指向其链接的颜色。文中提到的红黑树均为此种实现。

红黑树的定义：

  • 红黑树是一棵二叉树，结点间的链接分为红链接和黑链接两种
  • 红链接均为左链接
  • 没有任何一个结点同时与两条红链接相连
  • 任意空链接到根结点的路径上的黑链接数量相同（完美黑色平衡）

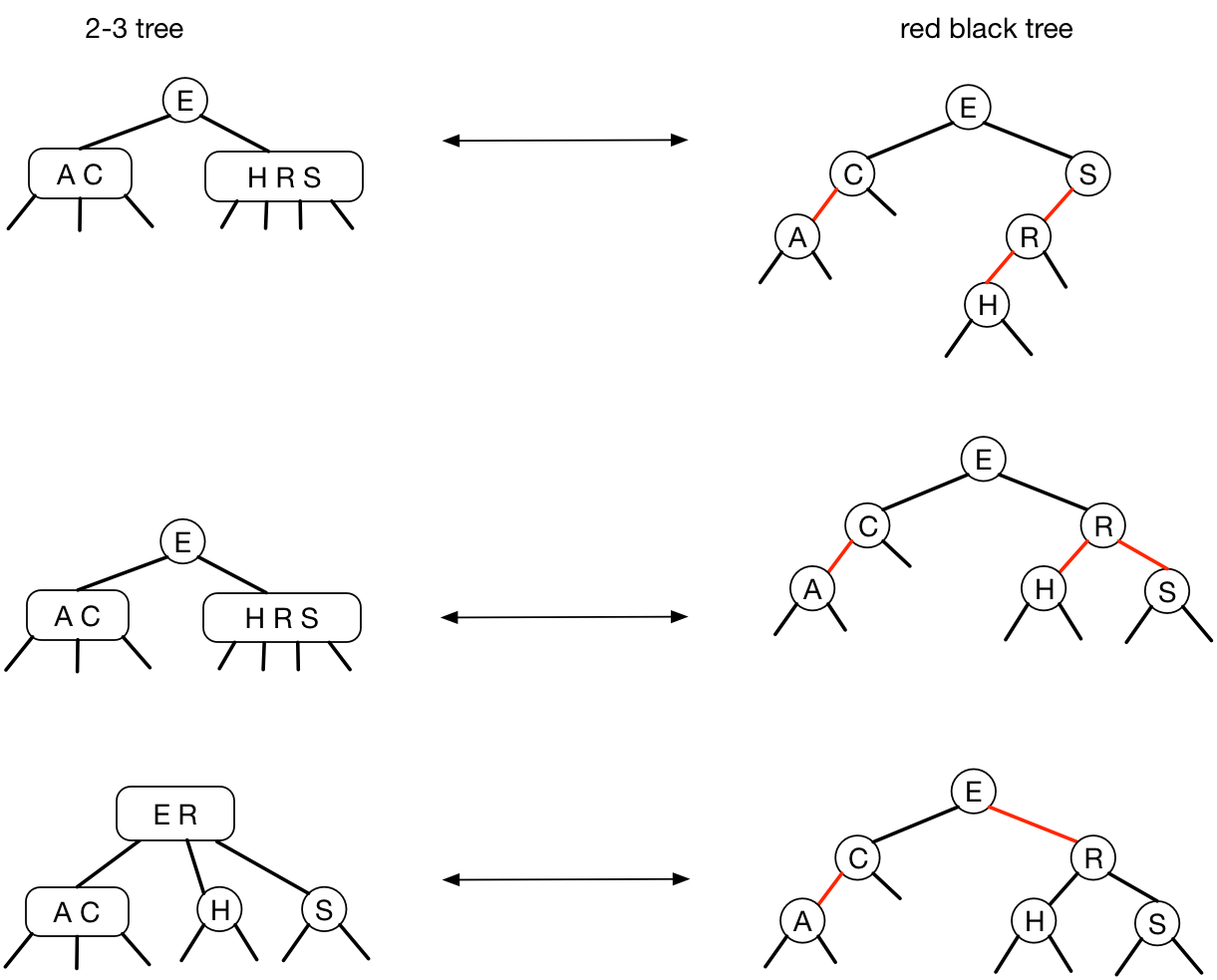
「2-3-4 树」与红黑树的对应关系：

  • 「2- 结点」：指向其的链接、左链接均为黑色
  • 「3- 结点」：由一个红链接两端的结点组成
  • 「4- 结点」：有两条红链接连接的三个结点组成
2-3 tree - red black tree relation (illegal cases)

每次插入一个新结点时，父结点指向新结点的链接为红色。为了保证红黑树的性质，需要利用「旋转」(rotate)和「颜色反转」(flip color)对红黑树进行一定的变换。

变换

旋转

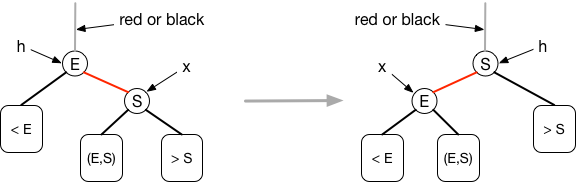Rotate Left 
1
2
3
4
5
6
7
8
9
10
11
// make a right-leaning link lean to the left
Node* rotateLeft(Node* h) {
    Node* x = h->right;
    h->right = x->left;
    x->left = h;
    x->color = h->color;
    h->color = RED;
    x->n = h->n;
    h->n = size(h->left) + size(h->right) + 1;
    return x;
}
Rotate Right 
1
2
3
4
5
6
7
8
9
10
11
// make a left-leaning link lean to the right
Node* rotateRight(Node* h) {
    Node* x = h->left;
    h->left = x->right;
    x->right = h;
    x->color = h->color;
    h->color = RED;
    x->n = h->n;
    h->n = size(h->left) + size(h->right) + 1;
    return x;
}

颜色反转

Flip Color 
1
2
3
4
5
6
7
8
9
// flip the colors of a node and its two children
void flipColors(Node* h) {
    assert(h != NULL && h->left != NULL && h->right != NULL);
    assert((!isRed(h) && isRed(h->left) && isRed(h->right) ||
            isRed(h) && !isRed(h->left) && !isRed(h->right)));
    h->color = !h->color;
    h->left->color = !h->left->color;
    h->right->color = !h->right->color;
}

插入情况分析

向树底部的 2- 结点插入

Insert into a single 2-node

向一棵双键树（即一个 3- 结点）插入

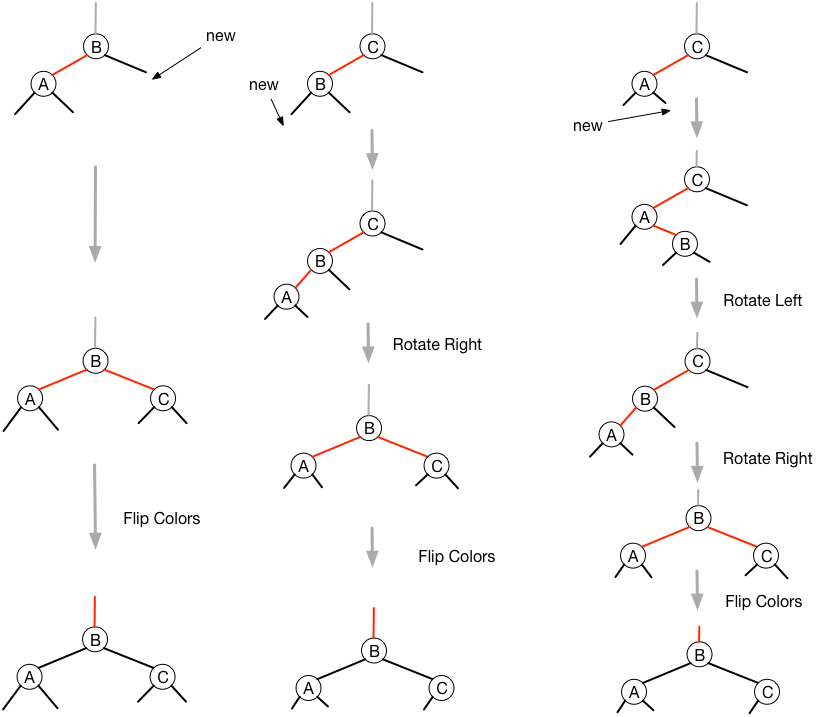Insert into a tree with two keys (in a 3-node)

向树底部的 3- 结点插入

会出现上面「向一棵双键树插入」讨论的三种情况，对应处理后把红链接传递到父结点递归处理。

插入结点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void put(K key, V val) {
    root = put(root, key, val);
    root->color = BLACK;
}

Node* put(Node* node, K key, V val) {
    if(node == NULL) return new Node(key, val, 1, RED);
    if(key < node->key) node->left = put(node->left, key, val);
    else if(key > node->key) node->right = put(node->right, key, val);
    else node->val = val;

    // fix-up any right-leaning links
    if(isRed(node->right) && !isRed(node->left)) node = rotateLeft(node);
    if(isRed(node->left) && isRed(node->left->left)) node = rotateRight(node);
    if(isRed(node->left) && isRed(node->right)) flipColors(node);

    // update size
    node->n = size(node->left) + size(node->right) + 1;
    return node;
}