红黑树实现（二）

Posted on Edited on Disqus:

Algorithms 4th RedBlackBST.java

红黑树介绍及其实现：删除结点实现

查找、获取最小结点

红黑树中查找（get）、获取最小结点（min）等基本读取操作与 BST 中完全一样，因为接下来的删除操作会用到这些函数，这里提一下，不赘述了。

删除结点

维基百科上的红黑树删除实现是先删除找到的结点，再考虑各种情况重新维护红黑树的平衡，这种方法不利于理解，而且容易出现错漏。'Algorithms 4th' 一书中根据红黑树与「2-3 树」一一对应的原理，讨论了「2-3 树」删除结点的情况，再类比到红黑树中实现。

删除最小键

  1. 「2-3 树」中的情况

    最小键位于树最左端的结点，显然在树的底部。从树底部删除「3- 结点」很简单，而删除「2- 结点」时会留下一个空链接，从而破坏树的平衡性。于是为了保证不会删除一个「2- 结点」，需要完成以下两步：

    1. 沿着左链接向下一路变换，以确保当前结点不是「2- 结点」。
    2. 在变换的过程中，会产生一些临时的「4- 结点」，需要在删除后回头一路分解它们。

    变换过程分为以下几种情况：

    1. 左子结点不是「2-结点」，跳过，递归访问左子结点。
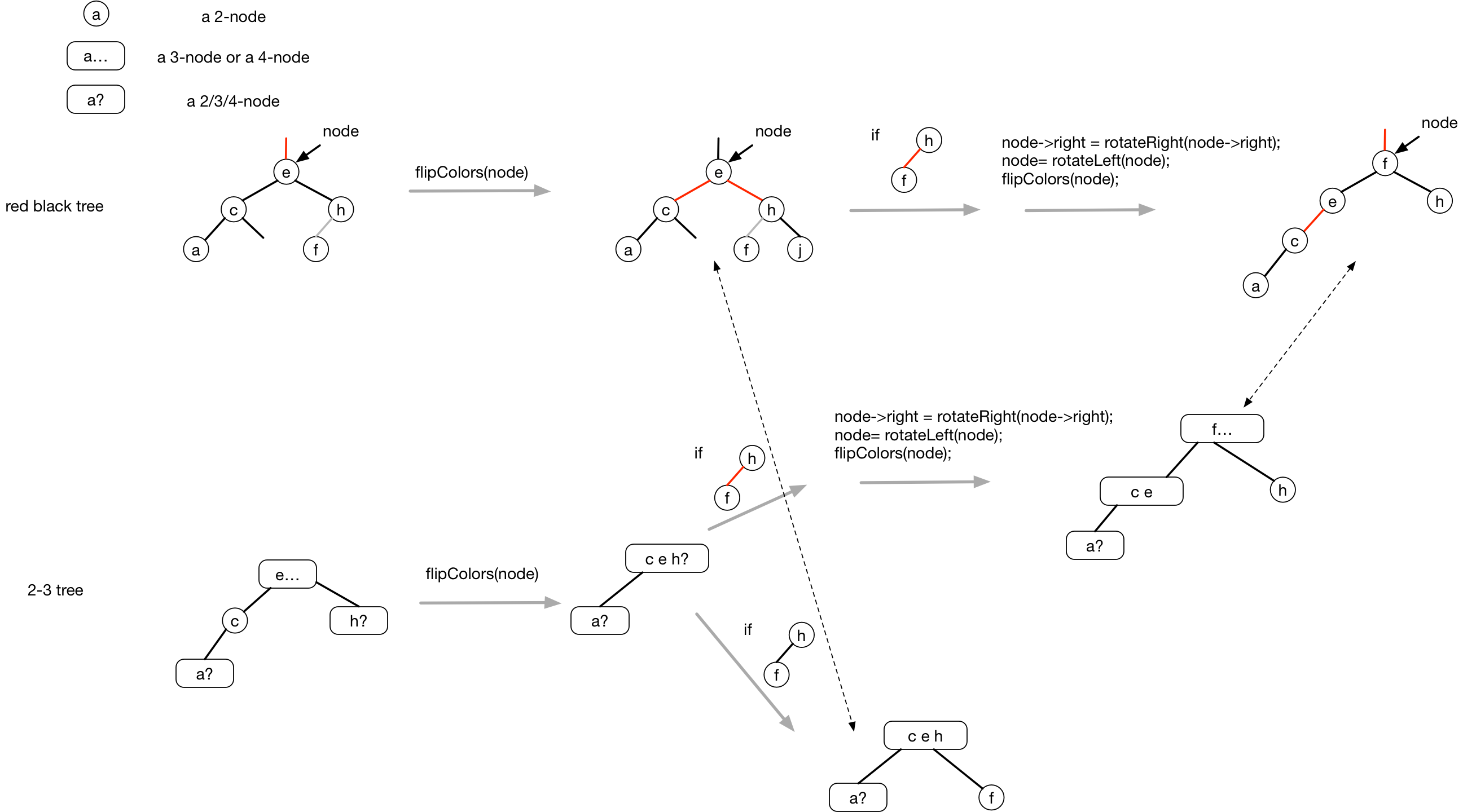
    2. 左子结点是「2- 结点」，而右子结点不是「2- 结点」，则从右子结点「借」一个键给左子结点。
    3. 两个子结点均为「2- 结点」，则将这三个结点合并为一个「4- 结点」。
    removeMin case 1 2-3tree
    removeMin case 2 2-3 tree

  2. 红黑树中的情况及实现

    在红黑树中我们要做的，就是利用「旋转」和「颜色反转」模拟「2-3 树」中的变换，保证当前结点不是「2- 结点」。在实现中体现为：在保证了当前结点不是「2- 结点」的基础上，通过变化使下一个访问的结点不是「2- 结点」，再递归访问。

    removeMin red black tree 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    // Assuming that h is red and both h.left and h.left.left
    // are black, make h.left or one of its children red.
    Node* moveRedLeft(Node* h) {
        // case 3: merge 3 2-nodes into a 4-node
        flipColors(h);

        /* case2: node->right is not a 2-node, lend a key from left child to right child.
         * Merge left key of node into key of node->left,
         * merge left key of node->right into keys of node
         * Based on transformation of case 3
         */
        if(isRed(h->right->left)) {
            h->right = rotateRight(h->right);
            h= rotateLeft(h);
            /* Not shown in the code of Algorithms 4th
             * will be done by function 'balance' if not do here
             */
            flipColors(h);
        }
        return h;
    }
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    void removeMin() {
        if(!isRed(root->left) && !isRed(root->right))
            root->color = RED;
        root = removeMin(root);
        if(!isEmpty()) root->color = BLACK;
    }

    Node* removeMin(Node* node) {
        if(node->left == NULL) {
            // if node->left == NULL, then node->right == NULL is true as well
            delete node;
            return NULL;
        }
        // case 1 not satisfied: node->left is a 2-node
        if(!isRed(node->left) && !isRed(node->left->left))
            node = moveRedLeft(node);
        node->left = removeMin(node->left);
        return balance(node);
    }

    删除结点后，退出调用栈的过程中，一步一步分解之前产生的「4- 结点」。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    // restore red-black tree invariant
    Node* balance(Node* h) {
        assert(h!= NULL);

        if(isRed(h->right)) h= rotateLeft(h);
        if(isRed(h->left) && isRed(h->left->left)) h= rotateRight(h);
        if(isRed(h->left) && isRed(h->right)) flipColors(h);

        h->n = size(h->left) + size(h->right) + 1;
        return h;
    }

删除最大键

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void removeMax() {
    if(!isRed(root->left) && !isRed(root->right))
        root->color = RED;
    root = removeMax(root);
    if(!isEmpty()) root->color = BLACK;
}

Node* removeMax(Node* node) {
    if(isRed(node->left)) node = rotateRight(node);
    if(node->right == NULL) {
        delete node;
        return NULL;
    }
    if(!isRed(node->right) && !isRed(node->right->left))
        node = moveRedRight(node);
    node->right = removeMax(node);
    return balance(node);
}

删除结点

把以上两种方法融合到 BST 的删除思路中，便得到了红黑树中删除结点的实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
// combine removeMin and removeMax
void remove(K key) {
    if(!contains(key)) return;
    if(!isRed(root->left) && !isRed(root->right))
        root->color = RED;
    root = remove(root, key);
    if(!isEmpty()) root->color = BLACK;
}

Node* remove(Node* node, K key) {
    if(key < node->key) {
        if(!isRed(node->left) && !isRed(node->left->left))
            node = moveRedLeft(node);
        node->left = remove(node->left, key);
    } else {
        if(isRed(node->left))
            node = rotateRight(node);
        if(key == node->key && node->right == NULL) {
            delete node;
            return NULL;
        }
        if(!isRed(node->right) && !isRed(node->right->left))
            node = moveRedRight(node);
        if(key == node->key) {
            Node* minNodeFromRight = min(node->right);
            node->val = minNodeFromRight->val;
            node->key = minNodeFromRight->key;
            node->right = removeMin(node->right);
        } else {
            node->right = remove(node->right, key);
        }
    }
    return balance(node);
}