MLF Lecture 5 Training versus Testing

Posted on Edited on Disqus:

機器學習基石(Machine Learning Foundations)笔记第五弹

Theory of Machine Learning can be split into Two Central Question

\[\begin{aligned} \color{green}{\large\text{Two Central Question}} \end{aligned}\] \[\begin{aligned} & \text{for }\underbrace{\text{batch & supervised binary classification}}_{lecture 3}, \color{purple}{\underbrace{g \simeq f}_{ \text{lecture 1}} \Longleftrightarrow E_{out}(g) \simeq 0} \\\ & \text{achieved through} \color{orangered}{\underbrace{E_{out}(g) \simeq E_{in}(g)}_{ \text{lecture 4}}} \text{ and } \color{crimson}{\underbrace{E_{in}(g) \simeq 0}_{ \text{lecture 2}}} \end{aligned}\]

hieved through} \end{aligned}

所以机器学习的目的研究方向主要分为两部分：

  1. 保证 \(E_{out}(g)\) 与 \(E_{in}(g)\) 很接近
  2. 尽量减小 \(E_{in}(g)\)

其中 \(\color{blue}{\underbrace{M}_{|H|}}\) 是研究两个问题的关键之一

When it comes to infinite hypothesis set

Known

\[\begin{aligned} \mathbb{P}[\mid E_{in}(h) - E_{out}(h)\mid > \epsilon] \leq 2 exp(-2\epsilon^2N) \end{aligned}\]

Todo

  • establish \(\color{orangered}{\text{a finite quantity}}\) that replaces \(\color{orangered}{M}\)
  • justify the feasibility of learning for infinite M
  • study \(\color{orangered}{m_h}\) to understand its trade off for 'right' \(\mathcal H\) , just like M

我们希望能将 infinite 的 M 换成一个与 Hypothesis 有关的 \(\bf{m_h}\) ，控制不等号右边上界的范围

Overestimation of Union Bound

在计算 \(\mathbb P \left[|E_{in}(g) - E_{out}(g)| > \epsilon \right]\) 时（我将其称为 \(E_{in}(g)\) 与 \(E_{out}(g)\) 的偏离概率），我们进行了放缩:

\[\begin{aligned} \mathbb P [B_1\ or B_2\ or \dots B_M]\color{orangered}{\underbrace{\leq}_{union\ bound}} \mathbb P [B_1] + \mathbb P[B_2] + \dots \mathbb P [B_M] \end{aligned}\]

然而实际情况是，由于 Hypothesis 中由许多极其相似的 h，所以每个 Bad Data 代表的范围有很大一部分是重合的，所以我们在使用 union bound 放缩时，

把重叠的主要部分都算进去了，导致对上界的过度估计。

Effective Line Numbers

我们先研究在二维平面内，对数据 \(x_1,x_2,\dots x_n\) 来说，有效的线段(effectice lines)有哪几种。

Effective Lines: 将数据分成 Ο 或 X 的线，划分后数据状况一样的线都是同一种 Effective Line

  • N = 1: 2 kinds
N = 1

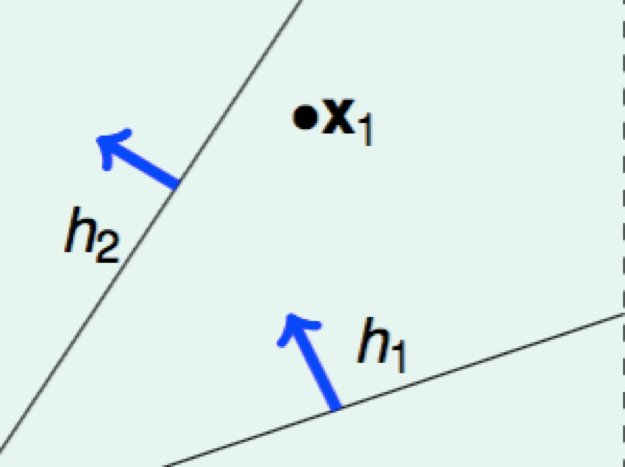
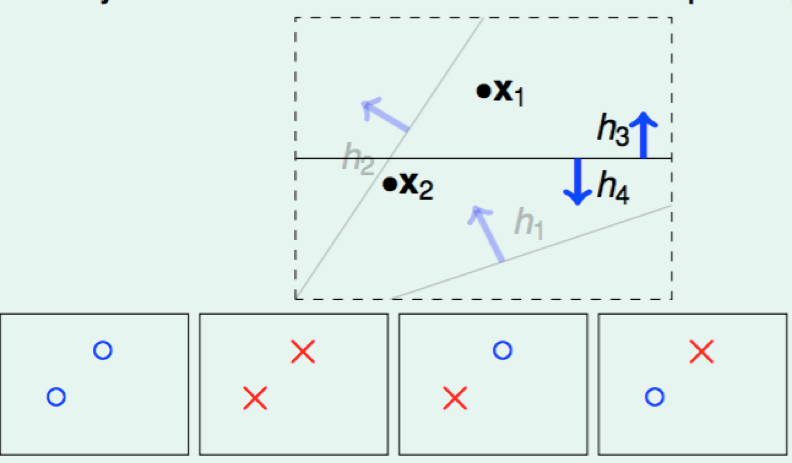
  • N = 2: 4 kinds

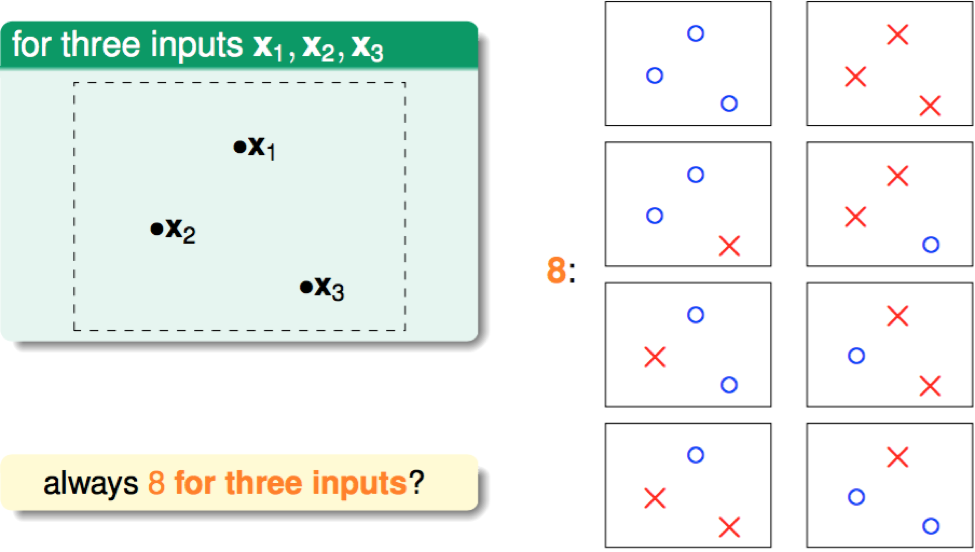
  • N = 3: max 8 kinds

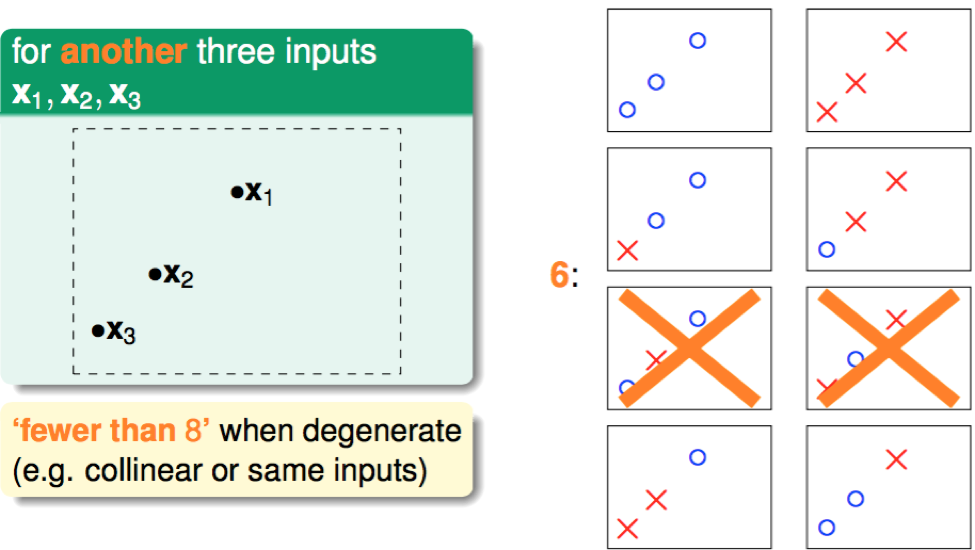
  • 三点共线: only 6 kinds

  • N = 4: max 14 kinds

    N = 4

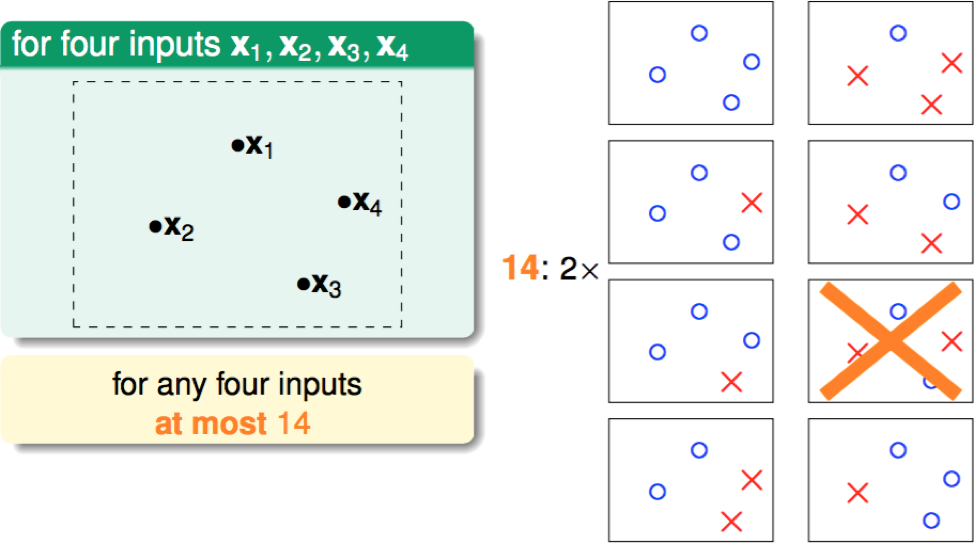
容易看出，对于 N 个数据，最多 \(2^N\) 种 Effective Lines（每个点的状态均有两种）

PS: 二维平面上 Kinds of Effective Lines

数法：分别输出 1 个相邻的点同状态，2 个相邻的点状态，... N 个相邻的点同状态的种数，然后相加。

因此，我们希望能够用关于 N 的成长函数（growth function）来取代 Hypothesis 的数量 M，当 effective(N)增长足够慢时且 N 很大时,即:

\[\begin{aligned} \mathbb P[|E_{in}(g) - E{out}(g)| > \epsilon] \leq 2 \cdot \color{orangered}{effective(N)} \cdot exp(-2\epsilon^2N) \quad (effective(N) \ll 2^N) \end{aligned}\]

\(E_{in}\) 与 \(E_{out}\) 的偏离概率足够小，从而使 Machine Learning 可能。

Dichotomy(二分法)

Growth Function

定义：数据量为 N 的所有数据情况中 Hypothesis 种类数量最多 \(\large m_h(N)\) 最大的函数

含义：为了摆脱 \(\large m_h(N)\) 对一定数据量 N 下数据不同排列组合情况的依赖

Growth Function

关于四种情况下增长函数的详细内容参见第五章课件

Break Point

shatter: Hypothesis 种类 = 2N 的情况

Break Point（突破点）： 使得当前数据无法出现 shatter 的 N 的值

比如二维的 perceptrons 下，N = 4 时 Hypothesis 种类最多为 14 < 24

Break Point of H