MLF Lecture 6 Theory of Generalization
機器學習基石(Machine Learning Foundations)笔记第六弹
Restriction of Break Point
受最小突破点 k 的限制,随着 N 增大, \(m_h(N) \ll 2^N\) ,下面通过画图枚举 dichotomies( \(x_1,x_2 \dots x_n\) 数值(O 或 X)的排列组合),研究 \(m_h(N)\) 受 k 的限制情况
\(N = 3, k = 2\) 的时候,可以找到一个 4 dichotomies 的"解"(不唯一)满足任意 两个 \(x\) 组合不发生 shatter 的情况:
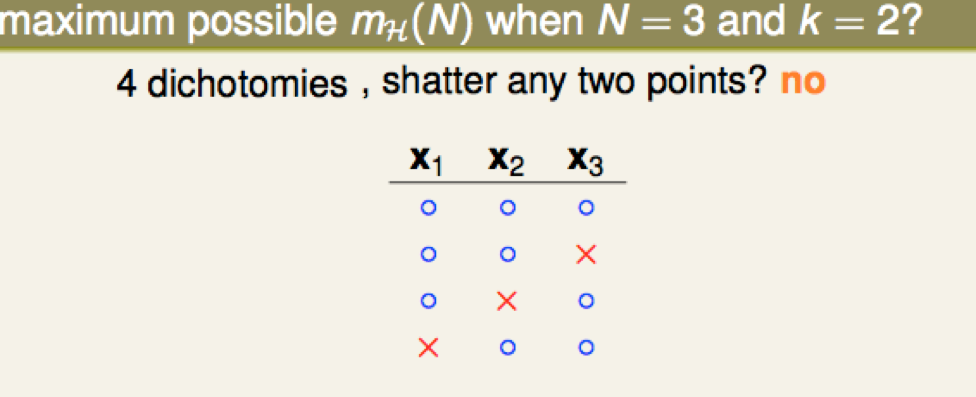
而 5 dichotomies 一定无法满足条件:

Table of Bound Function
为了进一步研究 k 对 \(m_h(N)\) 的限制性质,并试图发现其间的函数关系,我们定义 bounding function B(N,k) 代表 \(break point = k\) 下 \(m_h(N)\) 的最大值
于是我们得到 bounding function 的一张表
由以下性质可以得到表的右上部分:
- \(N < k\) 时, break point 的约束无效(N 个数据中选不出 k 个点),所以 \(B(N,k) = 2^N\)
- \(N = k\) 时,除了 N 个点不能**shatter**外无其他限制, \(B(N,k) = 2^N - 1\)
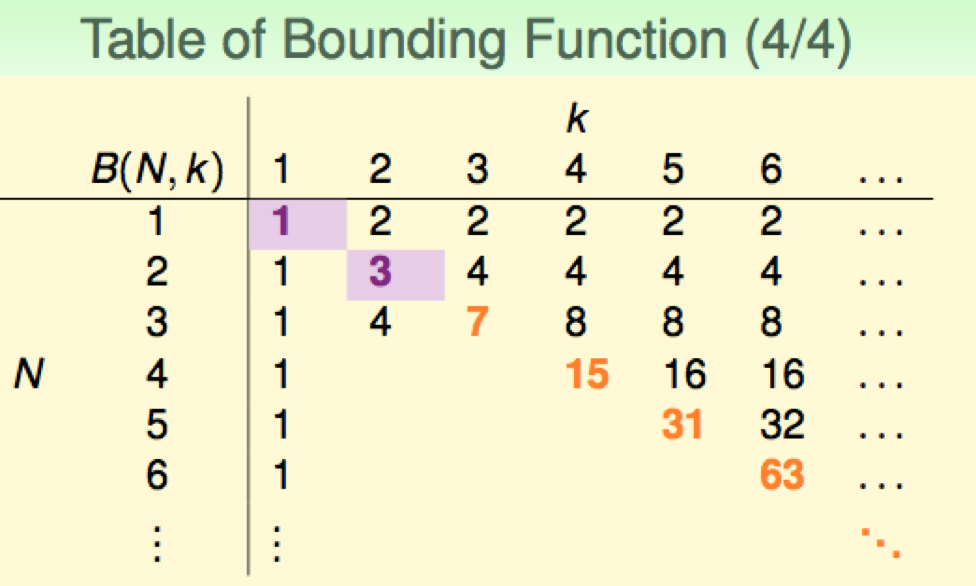
但关键的地方正是左下部分,很明显,这需要用递归的思想解决
Left Bottom Of Bound Table
下面的证明描述都只是大体的思路(sketch of proof)
以对 \(B(4,3)\) 为例,针对下图是这个解,我们可以 \(x_4\) 拆分出来,将 \(x_1,x_2,x_3\) 相同而 \(x_4\) 不同的分为一组(图中用橙色标出),组数 \(\alpha\) ;剩下的各自单独为一组(用紫色标出),组数 \(\beta\)
于是有 \(B(4,3) = 2\alpha + \beta\)
遮住 \(x_4\) 不看,去掉条重复的橙色条目,由 k=3 可知 \(\alpha + \beta < B(3,3)\)
具体见下图:
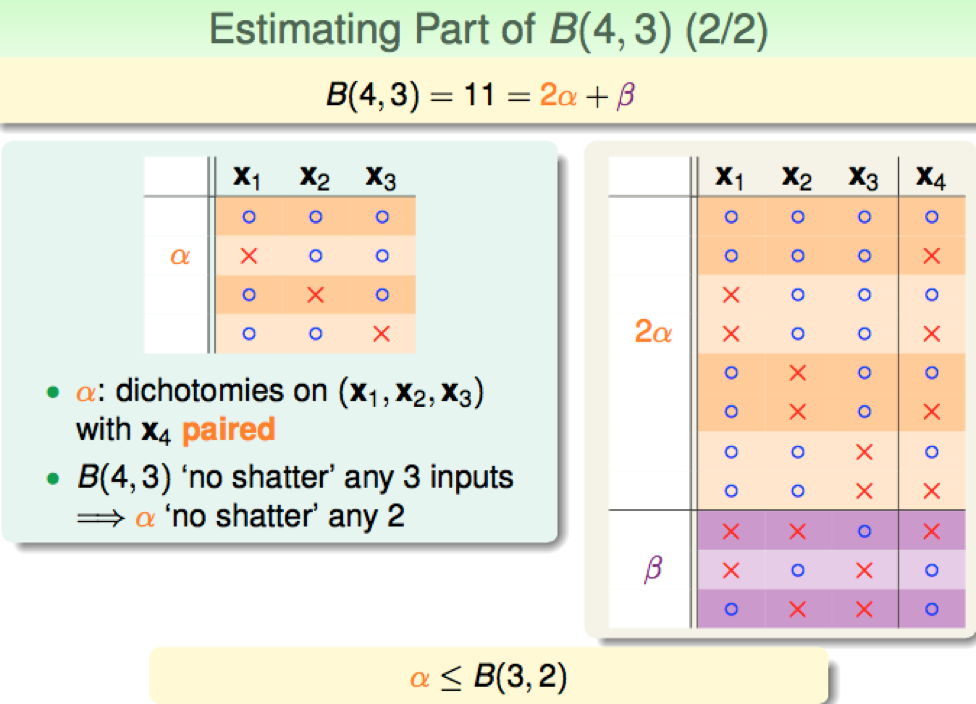
遮住 \(x_4\) 不看,再去掉紫色的部分,注意到如果 \(x_1,x_2,x_3\) 中存在两组 \(x\) 可以 shatter ,由于每个橙色条目一定对应 \(x_4\) 的两种情况,那么一定会存在 3 组 \(x\) 满足 shatter 的情况;所以此时 no "shatter" any 2
即: \(\alpha < B(3,2)\)
具体见下图:

用类似的方法,可以得到 B(N,k)的递推不等式: \(B(N,k) \leq B(N-1,k) + B(N - 1,k - 1)\)
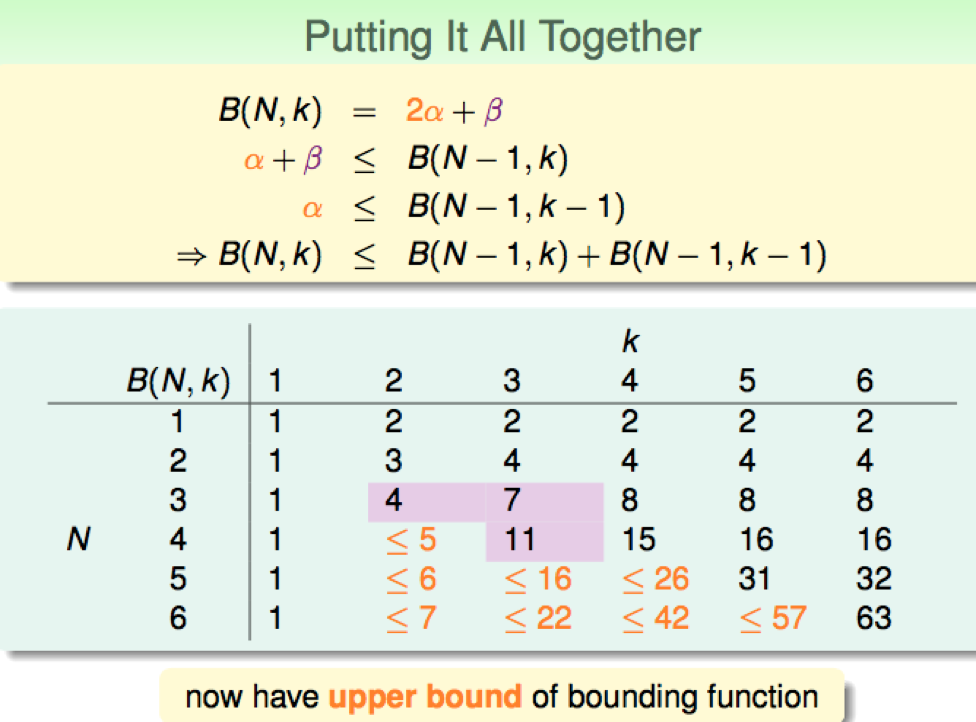
用数学归纳法可以证明:
\[\begin{aligned} B(N,k) \leq \sum_{i=0}^{k-1}\binom{N}{i} \end{aligned}\]这里用到二维的数学归纳法,步骤:
取 N, k 最小能取到的值,证明其满足条件
固定 N,证明 B(N,k)成立下 B(N+1,k)也成立
固定 k,证明 B(N,k)成立下 B(N,k+1)也成立
Bad Bound for General H
我们实际能证明的 Bad Bound 需要在原来设想的式子上增添一些常数
What we want:
\[\begin{aligned} \mathbb P \left [ \exists h \in \mathcal H s.t. |E_{in}(h) - E_{out}| > \epsilon \right] \leq 2 \color{coral}{m_{\mathcal H}(N)} \cdot exp(-2 \epsilon^2 N) \end{aligned}\]Actually, \(\color{red}{ \text{when N large enough}}\),
\[\begin{aligned} \mathbb P \left [ \exists h \in \mathcal H s.t. |E_{in}(h) - E_{out}| > \epsilon \right] \leq 2 \color{coral}{\cdot 2 m_{\mathcal H}(2N)} \cdot exp(-2 \cdot \frac{1}{16} \epsilon^2 N) \end{aligned}\]A Pictorial Proof
这一部分其实并不能算是证明,只是一个结合图形的说明。
Step 1: Replace \(E_{out}\) by \(E'_{in}\)
为了将 infinite 的 \(E_{out}\) 用有限的量代替,我们假设还有一组测试数据 \(D'\) (ghost data),然后可以做出一张关于数据的概率分布图,两边的是 \(E'_{in}\) 和 \(E_{in}\) ,中间的是 \(E_{out}\)
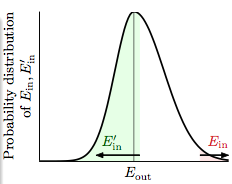
由图像及数学证明可得,属于 \(E'_{in}\) 的面积大于 1/2,可以得 \(E_{in} - E_{out} > \epsilon\) 的 \(\frac{1}{2}\) 不超过 \(E_{in} - E'_{in} > \frac{\epsilon}{2}\) 概率。
得:
\[\begin{aligned} & \color{red}{ \frac{1}{2} }\mathbb P \left[\exists h \in \mathcal H \space s.t.\left | E_{in}(h) - E_{out}(h) \right| > \epsilon \right] \\\ \leq \space & \mathbb P \left[ \exists h \in \mathcal H \space s.t. \left| E_{in}(h) - \color{red}{ E'_{in}(h) }\right| > \color{red}{\frac{\epsilon}{2}} \right] \end{aligned}\]ce & P \end{aligned}
于是我们完成了转化:
\[\begin{aligned} BAD \space h \space of \space E_{in} - E_{out} \color{red}{\overset{probably}\Longrightarrow BAD \space h \space of \space E_{in} - E'_{in}} \end{aligned}\]Step 2: Decompose \(\mathcal H\) by Kind
经过第一步的处理,**infinite** 的 \(\mathcal H\) 变为 \(\left| \mathcal H(x_1,\dots , x_N, x'_1, \dots, x'_N)\right|\) 种。再利用 ****union bound**** ,可以得这 2N 个点上的 Dichotomy 最多有 \(m_{\mathcal H}(2N)\) 种。
于是有:
\[\begin{aligned} BAD & \leq \color{red}{2} \mathbb P \left[ \exists h \in \mathcal H \space s.t. \left| E_{in}(h) - \color{red}{ E'_{in}(h) }\right| > \color{red}{\frac{\epsilon}{2}} \right] \\\ & \leq \color{red}{2} m_{\mathcal H}(2N) \mathbb P \left[ fixed \space h \space s.t. \left| E_{in}(h) - \color{red}{ E'_{in}(h)} \right| > \color{red}{\frac{\epsilon}{2}} \right] \end{aligned}\]color{red}{2} m_{H}(2N) P \end{aligned}
Step 3: Use Hoeffding without Replacement
这部分没有理解,就直接记录课件内容了 想象一个有 2N 个球的管子,取 N 个给 \(E_{in}\),留下的 N 个给 $E'in$,有:
\[\begin{aligned} \color{purple}{ |E_{in} - E'_{in}| > \frac{\epsilon}{2} \Longleftrightarrow |E_{in} - \frac{E_{in} + E'_{in}}{2}| > \frac{\epsilon}{4} } \end{aligned}\]这属于无放回的 Hoeffding,于是有:
\[\begin{aligned} BAD & \leq \color{red}{2} m_{\mathcal H}(2N)\mathbb P\left[fixed \space h \space s.t. |E_{in}(h) - color{red}{E'_{in}(h) }| > \color{red}{\frac{\epsilon}{2}} \right] \\\ & \leq \color{red}{2}m_{\mathcal H}(2N)\cdot 2exp\left(-2( \color{purple}{ \frac{\epsilon}{4}^2})N \right) \end{aligned}\]color{red}{2}m_{H}(2N)2exp(-2( )N ) \end{aligned}
Vapnik-Chervonenkis(VC) Bound
到此,我们成功得到了以下这个被称为 VC Bound 的不等式:
\[\begin{aligned} & \mathbb P \left[\exists h \in \mathcal H \space s.t. \left| E_{in}(h) - E{out}(h) \right| > \epsilon \right] \\\ \leq \space & \color{red}{4}m_{\mathcal H}(2B)exp \left(- \color{purple}{ \frac{1}{8}} \epsilon^2N \right) \end{aligned}\]ce & m_{H}(2B)exp (- ^2N ) \end{aligned}
对 2D perceptrons 来说,由于其 break point 为 4,所以 \(m_{\mathcal H}(N) = O(N^3)\) ,进而得到二维感知器的学习是可能的。